
从样本中提取有用的信息来研究总体的分布及各种特征数的过程叫做构造统计量
统计量:样本的不含任何位置参数的函数

常用统计量
基本概念
样本均值 样本方差 样本标准差 样本矩
样本均值和总体均值的区别

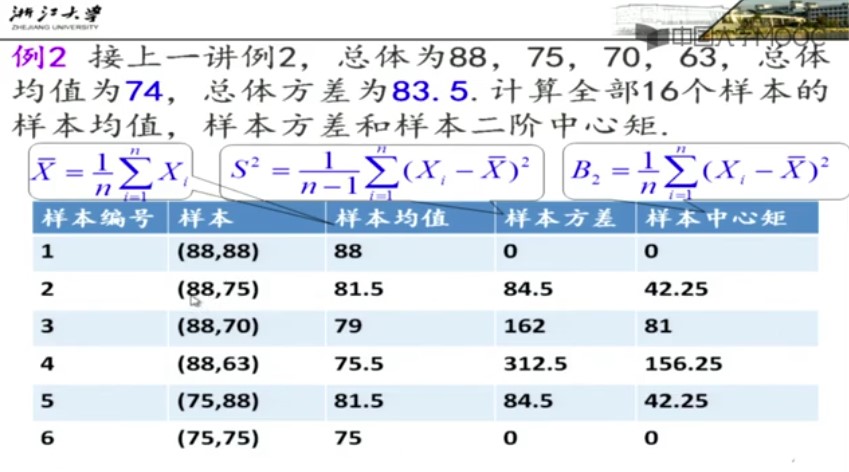
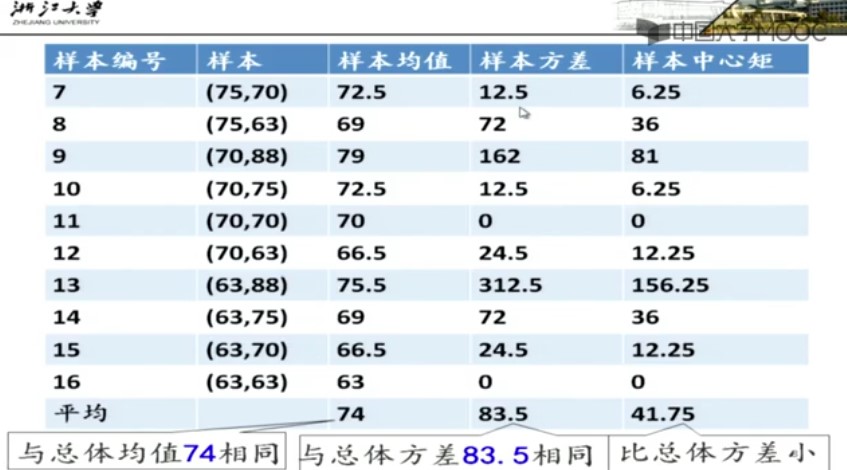
从上面的例子我们可以总结出这样的结论
样本均值的平均值等于总体均值 样本方差的平均值等于总体均值
当总体数字特征未知时,我们可以总结出以下的方法来求数字特征
- 用样本均值估计总体均值
- 用样本方差估计总体方差
- 用样本原点矩估计总体原点矩
- 用样本中心矩估计总体中心矩
统计量的分布被称为抽样分布
总体服从一般分布,如指数分布均匀,分布等要得出统计量的分布是很困难的 总体服从正态分布时统计量样本均值样本方差是可以计算的
直方图
方法:
- 求最大最小值,并求极差
- 分组定组距(一般数据个数n>=50,分成10组以上;小于的时候,一般分为5组)
- 定分点定区间
- 统计数据落入各组间的概率
- 画出直方图
作图反应数据特征