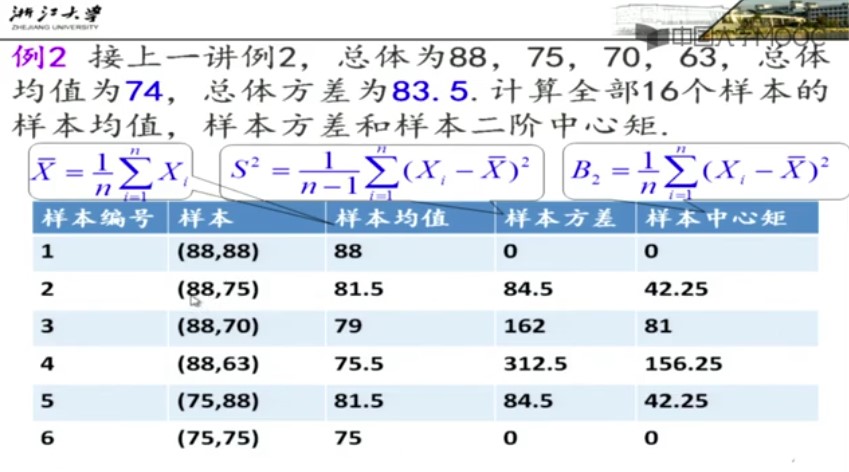
第一章:随机事件及其概率(1)
第一部分
样本空间,随机事件
来自百度百科
样本空间
####### 随机事件E的所有基本结果组成的集合为E的样本空间。样本空间的元素称为样本点或基本事件
####### 举个例子:设随机试验E是"抛一颗骰子,观察出现的点数"。那么E的样本空间就是S:{1,2,3,4,5,6,}。
####### 有些实验有两个或多个可能的样本空间。
######## 举个例子:从52张扑克牌中随机抽出一张,一个可能的样本空间是数字(A到K),另外一个可能的样本空间是花色(黑桃,红桃,梅花,方块)。 如果要完整地描述一张牌,就需要同时给出数字和花色,这时的样本空间可以通过构建上述两个样本空间的笛卡尔乘积来得到。
随机事件
####### 子主题 4
######## 随机事件是指在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件)
######## 随机试验中的每一个可能出现的试验结果称为这个试验的一个样本点,全体样本点组成的集合称为这个试验的样本空间。
######## 仅含一个样本点的随机事件称为基本事件 含有多个样本点的随机事件称为复合事件
#######
####### 特点
######## 1、可以在相同的条件下重复进行
######## 2、每个试验的可能结果不止一个,并且能实现预测试验的所有可能结果
######## 3、进行一次试验之前不能确定哪一个结果会出现
####### 特殊事件
######## 必然事件
######### 必然事件记作Ω,样本空间Ω也是其自身的一个子集,Ω也是一个"随机"事件,每次试验中必定有Ω中的一个样本点出现,必然发生。
######## 不可能事件
######### 不可能事件记作Φ,空集Φ也是样本空间的一个子集,Φ也是一个特殊的"随机"事件,不包含任何样本点,不可能发生。
####### 事件关系
######## 事件A是事件B的子事件,事件A发生必然导致事件B发生,事件A的样本点都是事件B的样本点,记作A⊂B。
######## 若A⊂B且B⊂A,那么A=B,称A和B为相等事件,事件A与事件B含有相同的样本点。
######## 和事件发生,即事件A发生或事件B发生,事件A与事件B至少一个发生,由事件A与事件B所有样本点组成,记作A∪B。
######## 积事件发生,即事件A和事件B同时发生,由事件A与事件B的公共样本点组成,记作AB或A∩B。
####### 事件种类
######## 互斥事件
######### 互斥事件(互不相容事件)事件A与事件B,AB=Φ,事件A与事件B不能同时发生,事件A与事件B没有公共的样本点。
######## 对立事件
######### 事件A的对立事件,事件A不发生,事件A的对立事件是由不属于事件A的样本点组成,记作ā。
######## 差事件
######### 差事件发生,即事件A发生且事件B不发生,是由属于事件A但不属于事件B的样本点组成,记作A-B。
来自维基百科
1.例子
####### 假设我们有一堆52张的扑克牌,并闭着眼睛在这堆牌中抽取一张牌,那么用概率论的术语来说,我们实际上是在做一个随机试验。这时,我们的样本空间是一个有着52个元素的集合,因为任意一张牌都是一个可能的结果。而一个随机事件,则是这个样本空间的任意一个子集(这个任意子集包括空集,一个元素的集合及多个元素的集合)。运用组合知识可以知道,随机事件一共有2\^52种。当这个事件仅仅包括样本空间的一个元素(或者说它是一个单元素集合)的时候,称这个事件为一个基本事件。比如说事件"抽到的牌是黑桃7"。当事件是空集时,称这个事件为不可能事件。当事件是全集时,则称事件是必然事件。其它还有各种各样的事件,比如: "抽到的牌是小丑"(也是不可能事件) "抽到的牌是红桃3"(基本事件) "抽到的牌数字是9"(包含4个元素) "抽到的牌是方块"(包含13个元素) "抽到的牌是红颜色的并且数字小于等于10"(包含20个元素) "抽到的牌不是红桃3"(包含51个元素) 由于事件是样本空间的子集,所以也可以写成集合的形式。有时候写成集合的形式可能会很困难。有时候也可以用文氏图来表示事件,这时可以用事件所代表图形的面积来按比例显示事件的概率。
事件的相互关系及运算
第二部分
等可能概型(古典概型)
基本描述
定义:古典概型也叫传统概率,其定义是由法国数学家拉普拉斯 (Laplace ) 提出的。如果一个随机试验所包含的单位事件是有限的,且每个单位事件发生的可能性均相等,则这个随机试验叫做拉普拉斯试验,这种条件下的概率模型就叫古典概型。
在这个模型下,随机实验所有可能的结果是有限的,并且每个基本结果发生的概率是相同的。古典概型是概率论中最直观和最简单的模型,概率的许多运算规则,也首先是在这种模型下得到的。
(1) 试验中所有可能出现的基本事件只有有限个;
####### 有限性
(2) 试验中每个基本事件出现的可能性相等。
####### 等可能性
具有以上两个特点的概率模型是大量存在的,这种概率模型称为古典概率模型,简称古典概型,也叫等可能概型。
古典概型的判断
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特征------有限性和等可能性,只有同时具备这两个特点的概型才是古典概型。
概率公式
P(A)= m/n =A包含的基本事件的个数m/基本事件的总数n
如果一次实验中可能出现的结果有n个,而且所有结果出现的可能性都相等,那么每一个基本事件的概率都是 1/n ; 如果某个事件A包含的结果有m个,那么事件A的概率为P(A)= m/n =A包含的基本事件的个数m/基本事件的总数n
条件概率
全概率公式与贝叶斯公式
事件独立性
第二章:随机变量及其分布(1)
第一部分
随机变量
离散型随机变量
分布函数
第二部分
连续型随机变量及其概率密度
均匀分布与指数分布
正态分布
随机变量函数的分布
第三部分
二元随机变量,离散型随机变量分布律
二元离散型随机变量边际分布律与条件分布律
不用看
二元随机变量分布函数、边际分布函数及条件分布函数
了解一下边缘分布函数即可
二元连续性随机变量,联合概率密度
自个笔记
子主题 1
第四部分
二元连续型随机变量边际概率密度
二元连续型随机变量条件概率密度
不用看
二元均匀分布,二元正态分布
随机变量的独立性
第五部分
二元随机变量函数的分布
Z=X+Y的分布
max(X,Y)和min(X,Y)的分布
第三章:随机变量的数字特征
第一部分
随机变量的数学期望
随机变量函数的数学期望
数学期望的性质
方差定义和计算公式
第二部分
方差的性质
协方差与相关系数
不相关与独立
矩,协方差矩阵,多元正态分布的性质